Concrete: Using manipulatives, real life objects like measuring tapes, base ten blocks, algebra tiles, fraction strips, cuisinaire rods, money, measuring cups, integer tiles, calipers, grid paper, protractors, timers, trundle wheels, clocks, counters, ten frames, rekenreks, etc.
Representational: Means making a representation, like drawing ten frames and integer tiles, using drawings of fractions, drawings of base ten blocks, graphs including graphing calculators, drawings of money, hash marks, etc.
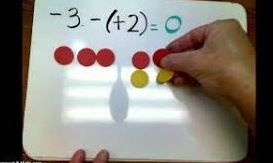
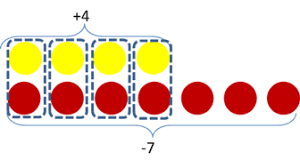
This example shows connecting the abstract (numbers) to the representation of integer tiles.
Abstract: Representing situations with numbers, equations, algrorithms, relations, and operations.
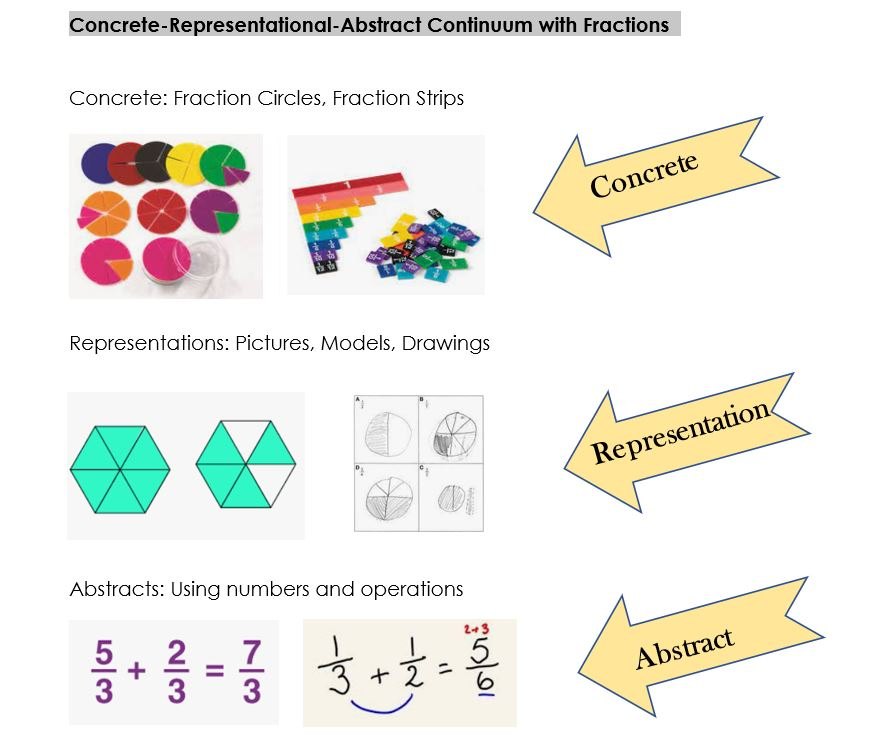
Fractions:
Teaching fraction and decimal multiplication and division Grades 7 and 8
Download this document:
Teaching Multiplication and Division of Fractions and Decimals
In the above video, there is a point where we should connect the concrete/pictorial to the abstract/representational
Here I would show the algorthim beside the picture, because the fact that we ended up with a "whole" shaded is the reason we "carry" the 1.
Area model multiplication:
This is the "overlapping shading" method. This is less concrete for kids
This is also "double shaded" method, but I like how he points out that "a part of a part is a smaller part"
This is also called "box multplication". Also less concrete.
Dividing decimals: this is nice and concrete--Partitive division
I can't find a good video of decimal division when there is a remainder so I made one.
How do I teach this? Check out this video collection of how to teach specific concepts http://fcit.usf.edu/mathvids/videos/videos.html

A whole website dedicated to Math Teaching Excellence. They have a lot to say about the importance of manipulatives.