What does it mean to do mathematics and learn mathematics? The National Council of Teachers of Mathematics, NCTM, describes “Mathematical processes” as the actions required to think mathematically. Our Saskatchewan Curriculum recognizes these processes as crucial to the teaching, learning and doing of mathematics.
Communication: Students need opportunities to speak and write about math in order to consolidate their understanding. “Communication helps students organize and reflect on their own mathematical thinking” (Glanfield, 2007). How many opportunities do we give students to talk?
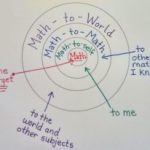
Connections: Mathematics is a continuum of learning, one concept built on another. Everything we understand in mathematics is built on our prior understanding. There is a rich and important connection between mathematical ideas—connections between symbols and procedures, and connections between math and the real world. If we teach math without exploring and highlighting these connections for students, we teach a set of discreet rules, piecemeal procedures that fosters memorization rather than understanding. Do we teach math as a series of discreet procedures and skills, or as a continuum of understanding?
Representing in math means to be able to draw models, graphs, equations, strategies, diagrams, words, and manipulatives. Math is visual communication, and symbolic representation is fundamental to math understanding. Representing is part of connections, communicating, and reasoning. In math, a picture really is worth a thousand words!
"Mathematics requires representations. In fact, because of the abstract nature of mathematics, people have access to mathematical ideas only through the representations of those ideas. Although on it's surface, high school mathematics may seem to be about facts and procedures, much of the real intellectual work in mathematics concerns the interpretation and use of representations of mathematical ideas." (National Research Council, 2001).
Visualization is the discipline that allows us to conceptualize number, pattern, and shape relationships. Visualizing mathematical meaning and connections is vital to finding an approach to a situation or problem, yet is often not explicitly taught. Having students communicate their reasoning fosters development of visualizing mathematical concepts. How can we use classroom dialog to explore and foster students’ visualization?
Reasoning: Mathematics is the discipline of reasoning. Mathematics is more than numbers: It is the language of if, then; the language of absolutes and situations, and of evidence and proof. Math teachers strive to help students develop confidence in their own reasoning abilities. By communicating, making mathematical connections, and creating representations, we foster students’ ability to reason. Logical reasoning is integral to mathematics, but applies to logic beyond mathematics. How do we support each student in developing an ability and desire to reason mathematically?
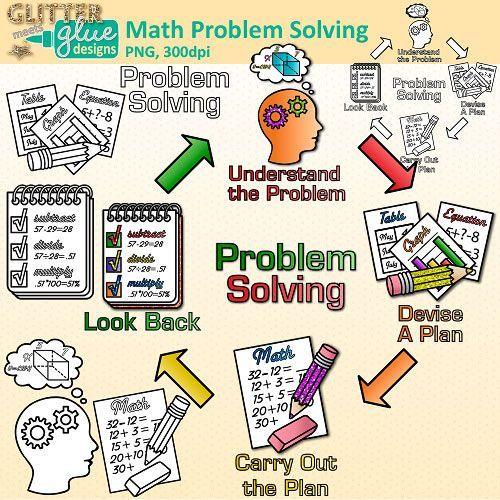
Problem solving refers to the ability to reason, visualize, make connections and representations to find a logical path to solutions. Students that are proficient problem solvers demonstrate an organization of reasoning accompanied by practiced strategies and persistence. Grit is an important attribute of successful math students and mathematicians. What can we do to foster grit in our students?
Technology is a tool that has greatly enhanced our understanding of mathematics. NCTM encourages use of calculators and software to explore, show relationships, provide pictorial representation, but cautions that calculators How do we use it in the classroom to promote and support learning, rather than to replace learning?